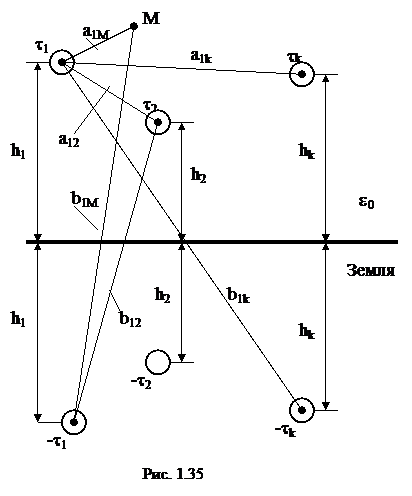
В виде примера, весьма важного для практики, рассмотрим систему из n заряженных проводов, протянутых параллельно друг другу над поверхностью земли (рис. 1.35). Линейная плотность заряда равна tk (индекс у заряда соответствует номеру провода). Высота подвеса и радиус каждого провода известны, а также известна диэлектрическая проницаемость e0 воздушной среды, окружающей провода. Возьмем в диэлектрике некоторую произвольную точку М (рис. 1.35) и найдем ее потенциал. Потенциал точки М будет равен сумме потенциалов, создаваемых каждым проводом и его зеркальным изображением.
Составляющую потенциала точки М от провода 1 и его зеркального изображения в соответствии с выражением, полученным в примере 9 раздела 1.14 можно записать следующим образом (постоянную, с точностью до которой определяется потенциал, опускаем):
![]()
(1.46)
где b1M – расстояние точки М до зеркального изображения первого провода; а1М – расстояние точки М до первого провода.
Будем полагать, что высота подвеса каждого провода над землей много больше радиуса проводов. При этом электрические оси практически совпадут с геометрическими осями.
Составляющую потенциала точки М от k -го провода и его зеркального изображения:
![]()
Таким образом,



