Решим задачу:
Дано: u(t) = Um sin wt; r; L; схема (рис. 2.10).
Найти: напряжение на индуктивности uL – ? и ток i – ?
Решение
Уравнение второго закона Кирхгофа имеет вид:
и является дифференциальным уравнением первого порядка. Найти указанные величины можно, но придется решать дифференциальное уравнение. Есть способ решения проще.
Использование комплексных чисел в расчетах цепей переменного тока
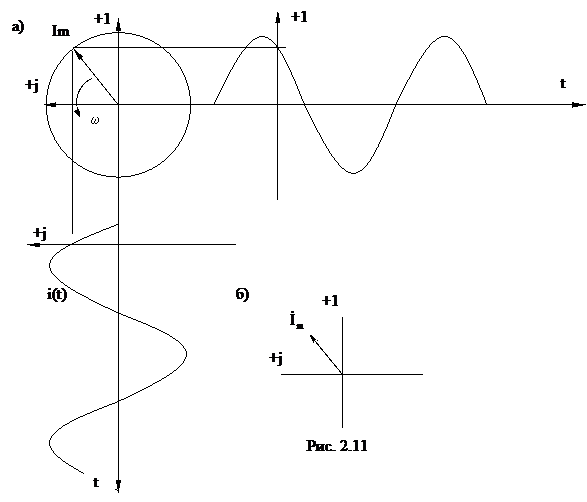
Представим синусоидально изменяющуюся величину вектором на комплексной плоскости (рис. 2.11). Для этого используем формулу Эйлера:
или для амплитуды тока:
.
Так как угол 
может быть любым, то
Из последней формулы видно, что мнимая часть равна мгновенному току.
Таким образом, если в мгновенный ток подставить момент времени t = 0, то на комплексной плоскости вращающийся отрезок останавливается в начальном положении. Этой информации достаточно для описания любой синусоидальной величины.
Например, ток i = 5 sin (
t +45) на комплексной плоскости (рис. 2.11, б)можно представить вектором:
,
где
– комплексная амплитуда тока.
Теперь дорешаем задачу. Дифференциальное уравнение
или с учетом подстановки напряжения 
при t = 0 в комплексном виде будет иметь вид:
Сопротивление Z = r + i XL называют комплексным.
Закон Ома в комплексной форме записи имеет вид:
.
Его используют для расчета токов в электрических цепях переменного тока. После расчета тока в комплексной форме можно перейти во временную область.
