Силовая цепь электромеханического преобразования энергии включает полупроводниковый преобразователь U, электродвигатель постоянного тока с независимым возбуждением M и промежуточную передачу механического движения рабочему органу механизма.
Полупроводниковый преобразователь в цепи якоря рассматривается как управляемый эквивалентный генератор ЭДС с внутренним активным сопротивлением и внутренней индуктивностью, не зависящими от нагрузки преобразователя. Ток нагрузки считается непрерывным; пульсирующие составляющие ЭДС и тока нагрузки преобразователя не учитываются.
Питающая сеть считается бесконечно мощной, т.е. связанные с изменением нагрузки колебания напряжения питания преобразователя отсутствуют. Двигатель постоянного тока с независимым возбуждением представляется в виде генератора противо-ЭДС с внутренним активным сопротивлением и индуктивностью, не зависящими от нагрузки. Влияние реакции якоря на возбуждение двигателя не учитывается.
Механическая часть рассматривается как абсолютно жесткая приведенная одномассовая система с постоянной величиной момента инерции. Предполагается, что момент статического сопротивления механизма содержит в общем случае реактивную и активную составляющие.
При построении математической модели силовой части приняты следующие условные обозначения параметров и сигналов :
К п – коэффициент усиления силового полупроводникового преобразователя в цепи якоря двигателя;
R я – суммарное активное сопротивление цепи якоря электропривода;
L я — суммарная индуктивность цепи якоря электропривода;
Тя = L я / R я — электромагнитная постоянная времени цепи якоря;
Тм = J R я /(CФ)2 — электромеханическая постоянная времени электропривода;
J — суммарный момент инерции механической системы;
С — конструктивная постоянная двигателя;
Ф — магнитный поток возбуждения двигателя;
Uу — управляющий сигнал на входе преобразователя;
Еп – ЭДС полупроводникового преобразователя;
Епм – максимальная ЭДС преобразователя;
Ед – противо -ЭДС якоря двигателя;
Iя – ток якоря двигателя;
М – электромагнитный момент двигателя;
Ώ – угловая скорость вращения якоря двигателя;
θ – угол поворота вала двигателя;
Мс – момент статического сопротивления механизма;
Ма – активная составляющая момента сопротивления механизма;
Мр – модуль реактивной составляющей момента сопротивления при движении механизма;
Мтр— модуль реактивной составляющей момента сопротивления при трогании механизма.
При этих условиях и допущениях математическая модель главной цепи электропривода описывается следующими уравнениями:
;
;
;
;
;
.
Первое уравнение описывает характеристику преобразователя как безынерционного управляемого источника питания в цепи якоря двигателя. Второе – это уравнение электрического равновесия цепи якоря. Последующие уравнения описывают связи электрической части с механической и движение последней.
Отметим существенную особенность моделирования нагрузки на валу элекродвигателя. Момент статического сопротивления механизма целесообразно представить как нелинейную функцию четырех переменных
.
Эта функция математически может быть выражена следующим образом
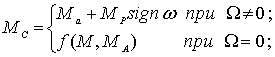
Вспомогательная нелинейная функция 
определяет полный момент сопротивления механизма в состоянии покоя (Мс=0). Здесь же дано условие трогания в случае превышения совокупности активных состовляющих момента (т.е. способных вызвать движ
ение механизма) М и нагрузки Ма над величиной реактивного момента трогания Мтр, обусловленного силами трения и неупругой деформации.
Очень часто параметры и переменные состояния электропривода представляются в относительных единицах. Общая формула перехода к относительным единицам имеет вид:
,
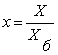где Х — значение физической величины (параметра, воздействия, переменной состояния и др.) в исходной системе единиц; Х6 — базисное значение, выраженное в той же исход
ной системе и принятое в качестве единицы измерения величины Х в системе относительных единиц; х – значение величины в системе относительных единиц.
За основные базисные величины для силовой части обычно принимают:
Тб = 1 c — время;
Uб = ЕЯ.Н — номинальная ЭДС якоря двигателя;
Iб=IЯН — номинальный ток якоря двигателя;
Фб = ФН — номинальный поток возбуждения;
Ώ6 = ΏН — номинальная скорость двигателя;
Мб = МН — номинальный электромагнитный момент двигателя.
Производные базисные величины:
Pб = Uб Iб – базисная мощность;
Rб = Uб/Iб — базисное сопротивление;
J6 = MбTб/Ώб — базисный момент инерции;
Θ = Ώб Тб – базисный угол поворота вала двигателя.
Для регулирующей части электропривода вводится собственная система базисных величин, соизмеримых с уровнями рабочих напряжений и токов элементов регулирующей части:
U б р << U б – базисное напряжение;
I б.р << I б — базисный ток;
R б.р = U б р / I б.р – базисное сопротивление.
Уравнения модели записанные в системе относительных единиц будут иметь вид:
;
;
;
;
;
.
В приведенных уравнениях относительные переменные определяются как:
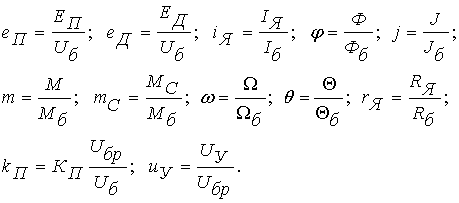
Отметим, что в дифференциальных уравнениях модели аргумент t выражен не в относительных, а в физических единицах. Это дает возможность изображать процессы в реальном времени и оперировать со следующими временными константами: ТЯ и Тj..
Первая константа представляет собой электромагнитную постоянную времени цепи якоря, а вторая – механическую постоянную времени электропривода. Эти константы характеризуют скорость протекания переходных процессов соответственно в главной цепи системы "преобразователь – двигатель" и в механической системе "электродвигатель – механизм". В частности, величина 
численно равна времени разгона механизма от состояния покоя до номинальной скорости под действием постоянного динамического момента, равного номинальному электромагнитному моменту двигателя.
Электромеханическая постоянная времени связана с механической постоянной времени соотношением
.
Структурная схема, соответствующая приведенным уравнениям показана на рис 3.1.
Рис. 3.1. Математическая модель силовой части электропривода
Представленная математическая модель характеризует силовую цель электропривода постоянного тока в общем случае как нелинейную систему с внутренней обратной связью по ЭДС. Модель приемлема для описания процессов, как при постоянном, так и при переменном возбуждении двигателя. В последнем случае она должна быть дополнена моделью цепи возбуждения.
